그래프(Graph)
그래프란 정점(Vertex)과 간선(Edge)로 이루어진 자료구조이다.
트리 또한 그래프이며, 트리는 사이클이 허용되지 않고, 그래프는 사이클이 허용된다.
- 사이클 : 그래프의 특정 정점에서 출발하여 돌아다니다가 다시 처음 출발했던 곳으로 되돌아 갈 수 있으면 사이클이 있다고 한다.
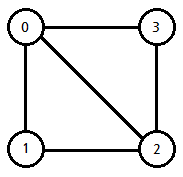
그래프 용어
- 정점 (Vertext, V) : 노드 라고도 하며 데이터가 저장되는 그래프의 기본 원소
- 간선 (Edge, E) : 정점(V, Node)를 연결하는 선, link, brach 라고도 부름
- 인접 정점 (adjacenct vertex, adj) : 간선에 의해 연결된 정점(그림 0, 3 등 이어진 정점)
- 단순 경로 (simple path) : 경로 중에서 반복되는 정점이 없는 경우. 동일한 간선을 지나가지 않는 경로
- 차수 (degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (0의 차수는 3 -> 1, 2, 3)
- 진출 차수 (out- degree) : 방향 그래프에서 한 정점에서 다른 정점으로
나가는간선의 수 - 진입 차수 (in - dgree) : 방향 그래프에서 외부에서 한 정점으로
들어오는간선의 수 - 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우.
그래프와 트리의 차이
그래프의 구현 방법
그래프는 구현할 때 행렬(인접행렬) 방식과 리스트(인접리스트) 방식으로 구현할 수 있다.
인접행렬 (adjacent matrix)
- 정방 행렬을 사용하는 방법
- 그래프의 노드를 2차원 배열로 행렬로 만든것
- 노드들간에 직접 연결되어있으면 1, 아니면 0을 넣어서 간선 연결 여부를 알 수 있음.
- 만약 가중치(거리 등)을 입력하는 그래프라면 해당 가중치 값을 넣어준다
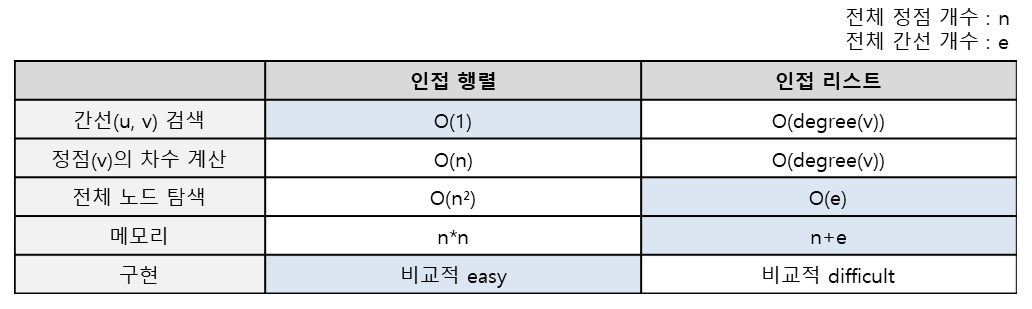
- 2차원 배열에 그래프 정점들의 정보가 모두 담겨있기 때문에 속도는 O(1)
장점
- 조회할 때 시간복잡도가 O(1)
- 구현이 쉽다
단점
- 모든 정점에 간선 정보를 대입해야 하므로 초기화할 때 O(n ^ 2) 시간이 소요된다
- 무조건 2차원 배열이기 때문에 메모리가 필요 이상으로 사용될 수 있다.
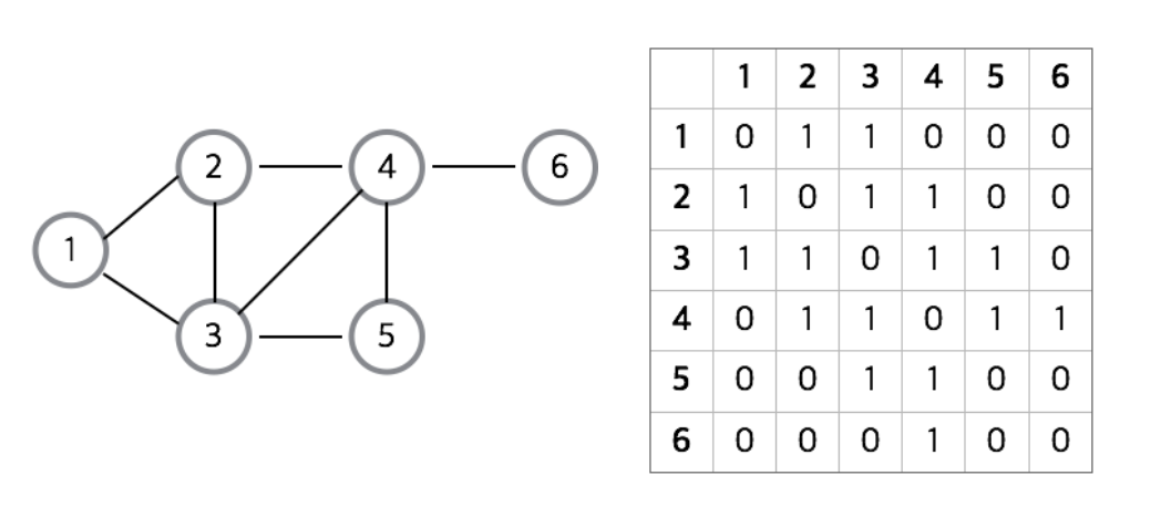
1번 노드와 1번 노드는 자기자신이므로 연결정보가 0
1번 노드와 3번 노드는 연결되어있으므로 연결정보가 1
1번 노드와 6번 노드는 연결되어있지 않으므로 연결정보가 0
인접리스트 (adjacent list)
- 연결 리스트를 사용하는 방법 (Linked List)
- 그래프의 노드를 연결리스트로 표현한것
- 정점마다 리스트 배열을 만들어 연결 정보를 알 수 있다.
- 장점
- 필요한 만큼의 메모리만 사용하기에 낭비가 적다
- 단점
- 정점들의 연결 정보를 탐색할 때 간선의 갯수만큼의 탐색이 필요하므로 O(n) 시간복잡도가 소요되어 인접행렬에 비해 시간이 오래 소요된다. O(E) = E는 간선 수 (O(n))
- 구현이 비교적 어렵다
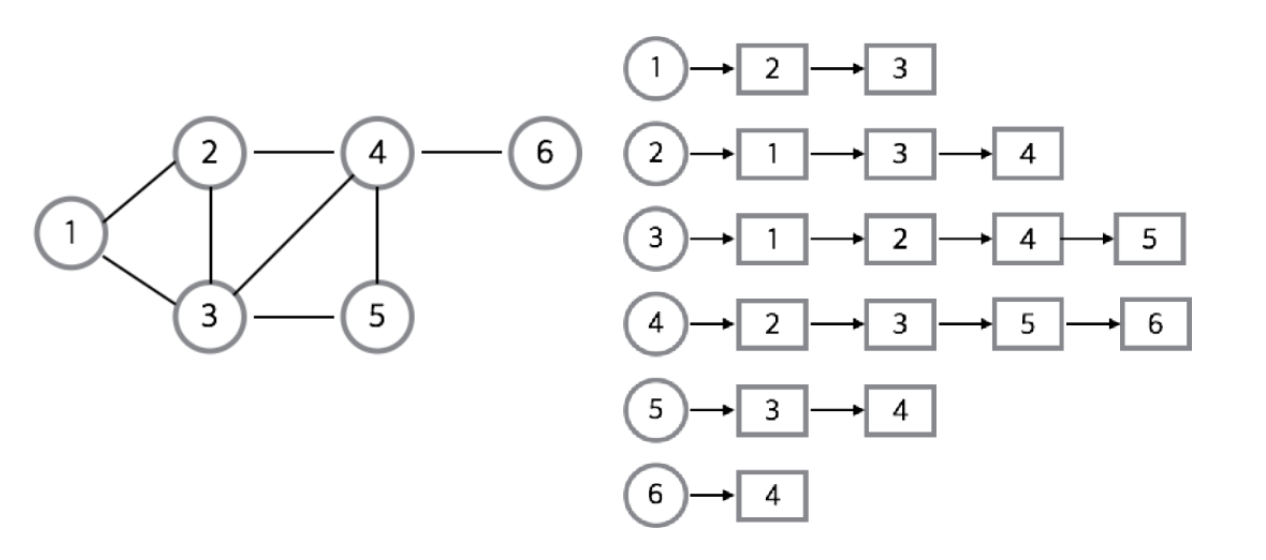
1번 정점은 2번 3번이랑 연결
3번 정점은 2번 3번 4번 5번이랑 연결
그래프의 종류
그래프는 간선에 방향을 표시할 수 있는 방향 그래프
방향이 없는 무방향 그래프
간선에 가중치가 존재하는 가중치 그래프
모든 정점사이에 간선이 존재하는 완전 그래프
무방향 그래프에서 모든 정점 쌍에 대해 항상 경로가 존재하는 연결 그래프
무방향 그래프 중에서 특정 정점 사이에 경로가 존재하지 않는 비연결 그래프 가 있다
무방향 그래프 - 두 정점을 연결하는 간선에 방향이 없는 그래프
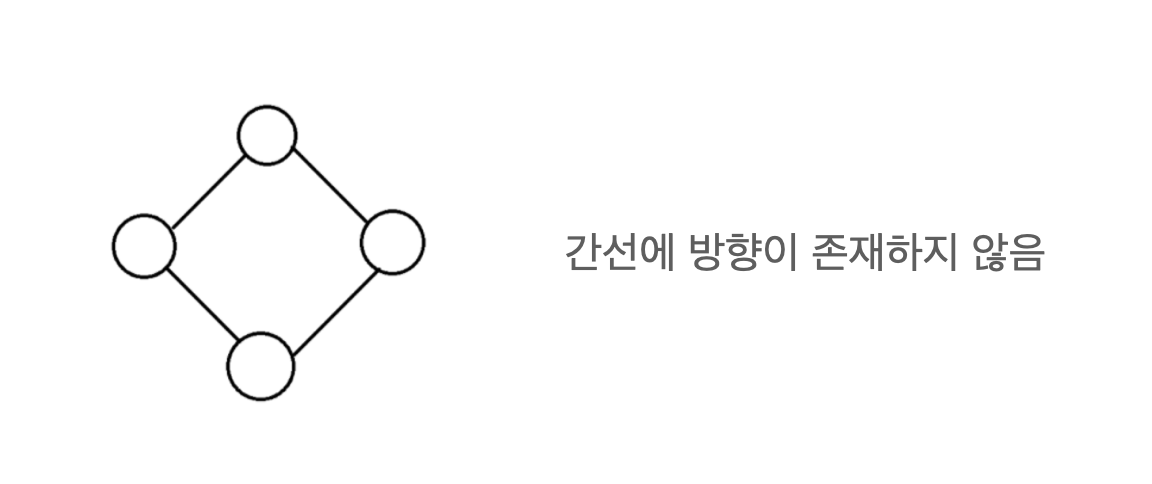
- 방향 그래프 - 두 정점을 연결하는 간선에 방향이 있는 그래프. 간선의 방향으로만 이동할 수 있다.

가중치 그래프 - 간선에 가중치가 존재하며, 정점 끼리 이동할 때 비용이 나온 그래프

- 완전 그래프 - 모든 정점사이에 간선이 존재하는 그래프. 고로 사이클도 무조건 존재
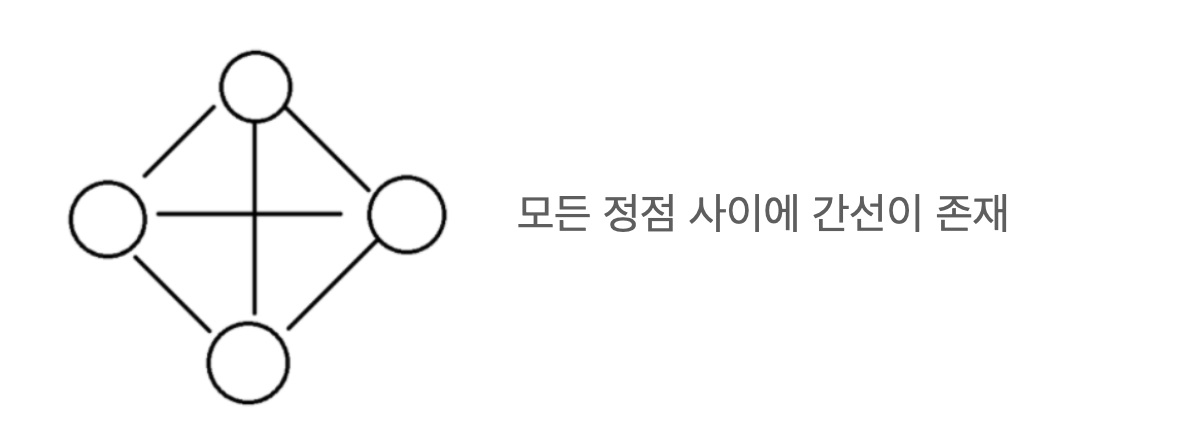
- 연결 그래프
- 무방향 그래프에 있는 모든 정점 쌍에 대해서 항상 간선이 연결되어 있어 경로가 존재하는 그래프
- 트리가 대표적인 예

- 비연결 그래프
- 무방향 그래프에서 특정 정점 사이에는 경로가 존재하지 않는 그래프
- 노드들 중 간선에 연결되어 있지 않은 노드가 존재하는 그래프

그래프의 탐색
그래프의, 모든 정점을 탐색하기 위한 방법은 2가지가 있다.
BFS(너비 우선 탐색 - Breadth First Search),
DFS(깊이 우선 탐색 - Depth First Search)
DFS, BFS를 활용하면 좋은 상황
DFS와 BFS를 활용하면 좋은 상황으로는 아래와 같은 상황들이 있다.
(1) 그래프의 모든 정점을 방문하는 것이 주요한 문제: DFS, BFS 모두 무방하다.
(2) 경로의 특징을 저장해둬야 하는 문제:
- 각 장점에 숫자가 있고 a 부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안된다는 문제 등,
- 각각의 경로마다 특징을 저장해둬야 하는 경우는 DFS를 사용해야 한다. BFS는 경로의 특징을 저장하지 못한다.
(3) 최단거리를 구하는 문제: BFS가 유리하다. DFS의 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만 BFS의 경우 먼저 찾아지는 해답이 곧 최단거리이기 때문이다.
- 미로찾기
(4) 재귀적이고 백트래킹을 이용하여 모든 경우를 하나하나 탐색하는 완전탐색 문제에서는 DFS가 유리하다.
- (조합, 순열 등)
BFS(너비 우선 탐색 - Breadth First Search)
넓게 탐색한다고 생각하면 된다.
그래프상의 한 정점으로부터 연결되어있는 모든 정점으로 나아간다.
Tree에서의 Level Order Traversal 형식이다(레벨 먼저 탐색 )
일반적으로 Queue를 사용한다
- 사용하는 경우 : 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을때 사용 ->
최단경로
BFS의 특징
재귀적으로 동작하지 않는다.
그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다 (검사하지 않을 경우 무한루프 가능성 있음 )
방문한 노드들을 차례대로 저장한 후 꺼낼 수 있는 자료구조인 큐(Queue)를 사용
- 선입선출(FIFO) 원칙으로 탐색
최단 경로를 찾기위해 사용한다.
DFS와의 가장 큰 차이로, 여러 갈래 중 무한한 길이를 가지는 경로가 존재하고 탐색 목표가 다른 경로에 존재하는 경우 DFS로 탐색할 시에는 무한한 길이의 경로에서 영원히 종료하지 못하지만, BFS의 경우는 모든 경로를 동시에 진행하기 때문에 탐색이 가능하다는 특징이 있다

진행순서
- 시작 노드를 방문하고 방문한 노드를 체크한다.
- 큐에서 꺼낸 노드와 인접한 노드들을 큐에 추가한다(모두 차례대로 방문)
- 큐에서 꺼낸 노드를 방문한다
- 큐에서 꺼낸 노드와 인접한 노드들을 모두 방문한다
- 인접한 노드가 없다면 큐의 앞에서 노드를 꺼낸다(dequeue)
- 큐에 방문된 노드를 삽입(enqueue)한다
- 큐가 공백상태가 될때까지 계속 반복한다
구현 방법
- 인접리스트(연결리스트로 된 배열 -> LinkedList[] adjList )
- 인접행렬(2차원 행렬) ->
int[][] adjArra;
정점의 개수에 비해 간선의 개수가 적은 그래프에서는 인접리스트가 유리할 수 있고.
모든 정점간 간선이 존재하는 완전그래프에서는 인접행렬이 유리할 수 있다.
상황에 따라 최대로 유리한 최선에 방법을 선택하는 것이 좋다.
Java 구현
Java BFS 인접리스트, 인접행렬 구현 - 접기/펼치기
public class Graph {
public static class AdjList {
private final LinkedList<Integer>[] adj;
private final int vertexCount;
public AdjList(int vertexCount) {
this.vertexCount = vertexCount;
adj = new LinkedList[vertexCount];
for (int i = 0; i < vertexCount; i++) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int v, int otherV) {
adj[v].add(otherV);
}
public List<Integer> bfs(int startVertex) {
boolean visited[] = new boolean[this.vertexCount];
Queue<Integer> queue = new LinkedList<>();
visited[startVertex] = true;
queue.add(startVertex);
List<Integer> visitOrder = new ArrayList<>();
while (!queue.isEmpty()) {
int visitVertex = queue.poll();
visitOrder.add(visitVertex);
for (int nextVertex : adj[visitVertex]) {
if (!visited[nextVertex]) {
visited[nextVertex] = true;
queue.add(nextVertex);
}
}
// 같은 방법
// Iterator<Integer> iterator = adj[visitVertex].iterator();
//
// while (iterator.hasNext()) {
// int nextVertex = iterator.next();
//
// if (!visited[nextVertex]) {
// visited[nextVertex] = true;
// queue.add(nextVertex);
// }
// }
}
return visitOrder;
}
}
public static class AdjArray {
private final int[][] adjArray;
private final int vertexCount;
public AdjArray(int vertexCount) {
this.vertexCount = vertexCount;
this.adjArray = new int[vertexCount][vertexCount];
}
public void addEdge(int vertex, int otherVertex) {
adjArray[vertex][otherVertex] = 1;
adjArray[otherVertex][vertex] = 1;
}
public List<Integer> bfs(int startVertex) {
List<Integer> visitOrder = new ArrayList<>();
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[vertexCount];
queue.add(startVertex);
visited[startVertex] = true;
while (!queue.isEmpty()) {
int visitVertex = queue.poll();
visitOrder.add(visitVertex);
for (int i = 0; i < adjArray[visitVertex].length; i++) {
if (adjArray[visitVertex][i] == 1 && !visited[i]) {
queue.add(i);
visited[i] = true;
}
}
// 같은 방식
// for (int i = 0; i < vertexCount; i++) {
// if (adjArray[visitVertex][i] == 1 && !visited[i]) {
// queue.add(i);
// visited[i] = true;
// }
// }
}
return visitOrder;
}
}
public static void main(String[] args) {
// 인접리스트
Graph.AdjList listGraph = new Graph.AdjList(4);
listGraph.addEdge(0, 1);
listGraph.addEdge(0, 2);
listGraph.addEdge(1, 2);
listGraph.addEdge(2, 0);
listGraph.addEdge(2, 3);
listGraph.addEdge(3, 3);
System.out.println(listGraph.bfs(2));
listGraph = new Graph.AdjList(5);
listGraph.addEdge(0, 1);
listGraph.addEdge(0, 2);
listGraph.addEdge(0, 4);
listGraph.addEdge(1, 2);
listGraph.addEdge(3, 4);
listGraph.addEdge(2, 3);
listGraph.addEdge(2, 4);
System.out.println(listGraph.bfs(0));
// 인접행렬
Graph.AdjArray arrayGraph = new Graph.AdjArray(4);
arrayGraph.addEdge(0, 1);
arrayGraph.addEdge(0, 2);
arrayGraph.addEdge(1, 2);
arrayGraph.addEdge(2, 0);
arrayGraph.addEdge(2, 3);
arrayGraph.addEdge(3, 3);
System.out.println(arrayGraph.bfs(2));
arrayGraph = new Graph.AdjArray(5);
arrayGraph.addEdge(0, 1);
arrayGraph.addEdge(0, 2);
arrayGraph.addEdge(0, 4);
arrayGraph.addEdge(1, 2);
arrayGraph.addEdge(3, 4);
arrayGraph.addEdge(2, 3);
arrayGraph.addEdge(2, 4);
System.out.println(arrayGraph.bfs(0));
}
}DFS (Depth First Search)
깊게 탐색.
연결된 노드들을 따라서 더 나아갈 길이 보이지 않을떄까지 깊이 들어간다.
루트 노드(정점) 혹은 다른 임의의 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 끝까지 탐색하는법
- 더 이상 연결된 노드가 없으면 시작한 노드에서 다른 노드로 이동.
모든 노드를 방문하고자 하는 경우에 사용.
자기 자신을 호출하는 순환 알고리즘(재귀 형태 )
- 스택 또는 재귀 함수로 구현
BFS 보다 좀더 간단하나 검색 속도 자체는 BFS보다 느리다
트리 순회(전위, 중위 ,후위 순회)는 모두 DFS의 한 종류
어떤 노드를 방문했었는지 여부를 반드시 검사 안하면 무한루프 빠질 위험이 있다.
진행순서
- a 노드(시작 노드라고 가정)를 방문하고 방문한 노드를 체크한다.
- a 노드의 인접한 노드들을 차례로 순회
- 방문한 노드와 인접한 노드가 없다면 종료
- a노드와 이웃한 노드 b노드를 방문했다면, a와 인접한 다른 이웃한 노드를 방문하기 전에 먼저 방문한 b노드의 인접 노드들을 전부 방문해야한다.
- b와 인접한 노드들을 전부 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안된 정점을 찾는다.
- 있으면 그 정점을 시작 정점으로 다시 DFS를 시작
- 모든 정점을 방문했으면 종료.
구현 방법
- 순환 호출 이용 - 재귀방법
- 스택 사용 - 인접한 정점들을 스택에 저장하였다가 사용
Java 인접리스트 - Stack, Recursiv 구현 - 접기/ 펼치기
public static class AdjList {
private int vertexCount;
private LinkedList<Integer> adj[];
private boolean[] visited;
public AdjList(int vertexCount) {
this.vertexCount = vertexCount;
adj = new LinkedList[vertexCount];
for (int i = 0; i < vertexCount; i++) {
adj[i] = new LinkedList<>();
}
visited = new boolean[vertexCount];
}
public void addEdge(int vertex, int otherVertex) {
adj[vertex].add(otherVertex);
adj[otherVertex].add(vertex);
}
public void dfsRecursive(int vertex) {
visited[vertex] = true;
System.out.println("visited -> " + vertex);
for (int next : adj[vertex]) {
if (!visited[next]) {
dfsRecursive(next);
}
}
// while (iterator.hasNext()) {
// int next = iterator.next();
//
// if (!visited[next]) {
// dfsRecursive(next);
// }
// }
}
public void dfsStack(int startVertex) {
Stack<Integer> stack = new Stack<>();
stack.push(startVertex);
visited[startVertex] = true;
while (!stack.isEmpty()) {
int vertex = stack.pop();
System.out.println("visited -> " + vertex);
for (int next : adj[vertex]) {
if (!visited[next]) {
stack.push(next);
visited[next] = true;
}
}
}
}
}Java 인접행렬 - Stack, Recursiv 구현 - 접기/ 펼치기
public static class AdjArray {
private int[][] adjArray;
private int vertexCount;
private boolean[] visited;
public AdjArray(int vertexCount) {
this.vertexCount = vertexCount;
adjArray = new int[vertexCount][vertexCount];
visited = new boolean[vertexCount];
}
public void addEdge(int vertex, int otherVertex) {
adjArray[vertex][otherVertex] = 1;
adjArray[otherVertex][vertex] = 1;
}
public void dfsRecursive(int vertex) {
visited[vertex] = true;
System.out.println("visited -> " + vertex);
for (int i = 0; i < adjArray[vertex].length; i++) {
if (adjArray[vertex][i] == 1 && !visited[i]) {
dfsRecursive(i);
}
}
}
public void dfsStack(int startVertex) {
Stack<Integer> stack = new Stack<>();
stack.push(startVertex);
visited[startVertex] = true;
while (!stack.isEmpty()) {
int vertex = stack.pop();
System.out.println("visited -> " + vertex);
for (int i = 0; i < adjArray[vertex].length; i++) {
if (adjArray[vertex][i] == 1 && !visited[i]) {
stack.push(i);
visited[i] = true;
}
}
}
}
}'CS > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] 해시, 해시테이블 (0) | 2022.08.15 |
|---|---|
| [자료구조] Heap 힙, 우선순위 큐 (0) | 2022.08.14 |
| [자료구조] 트리, B Tree, B+Tree (0) | 2022.08.14 |
| [자료구조] 트리, AVL 트리 (0) | 2022.08.14 |
| [자료구조] 트리, 레드블랙 트리 (Red-Black-Tree) (0) | 2022.08.14 |

